Cromovector, una solución innovadora para el color

Planteamiento del problema

En uno de nuestros proyectos con la empresa Centro Colores El Pintor, en el desarrollo de su Ecommerce, tuvimos un desafío importante. El fuerte de la empresa es la preparación exacta del color que el cliente pide entre la gran amplia gama disponible. Debíamos implementar una cartilla de colores, ya que, en Costa Rica, ninguna otra opción en el mercado, cuenta con la venta de pinturas con color a escoger. Solo las bases o sus color blanco por defecto.

Nuestro deber era hacer destacar a la empresa como la pionera en el mercado. Por ello, aplicamos nuestro ingenio. Escaneamos las cartillas de colores para digitalizarlas y mediante Computer Vision, extraer los datos pertinentes de cada color.

Teniendo esta base de datos de colores, logramos hacer que en los productos de pinturas, se pudiera seleccionar cualquiera de los 6000 colores que posee la empresa. Pero vimos un problema como si fueramos los clientes de la Web. Si quiero comprar varios colores, quisiera saber cuáles son los adecuados para el espacio que voy a pintar. Pero, ¿Cuáles son los colores adecuados? ¿Cuáles colores combinan? ¿Cuáles colores contrastan?.

Tuvimos que aplicar pensamiento abstracto para poder resolver este pequeño problema que se nos presentaba. Desacoplamos mentalmente la cartilla de colores de su acomodo tradicional.

Desacomodamos esta cartilla y la volvimos a estructurar de otra manera, en un espacio matemático basado en el espacio LAB del color, que llamamos Cromovector.

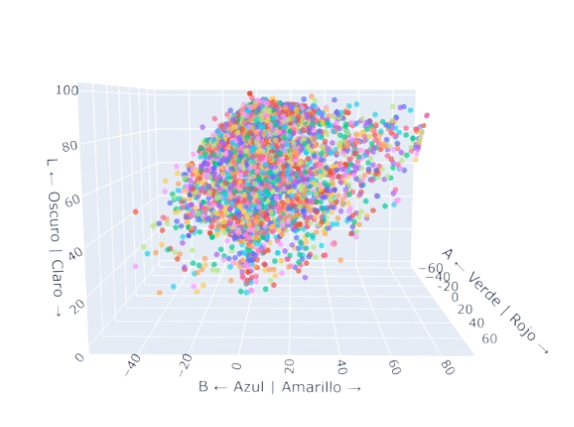
Estos 6000 puntitos, son las ubicaciones de cada color en este espacio de 3 dimensiones. Los cuales son

- Luminosidad del Color: [0, 100]
- Componente A (Verde - Rojo) ]-50, 50[
- Componente B (Amarillo - Azul): ]-50, 50[

Búsqueda de Sentido

Buscamos el sentido de los colores. ¿Por qué el color A combina con el color B? ¿Por qué contrastan? ¿Por qué se ven bien juntos? Buscamos las combinaciones proporcionadas por uno de los proveedores de color de la empresa. Nos brindaron paletas de colores generadas por expertos en el área. Las analizamos mediante un algoritmo matemático escrito en Python que dedujimos de la siguiente manera.

Consideramos el espacio de color CIELAB, un espacio tridimensional aproximadamente perceptualmente uniforme, donde cada color se representa mediante el vector:

$$\vec{C} = (L, A, B)$$

Tratamos el espacio de color como un espacio métrico, donde cada color es un punto y la relación entre colores se evalúa mediante distancias.

Definido por:

$$d(\vec{C}_1,\vec{C}_2) = \sqrt{(L_2 - L_1)^2 + (A_2 - A_1)^2 + (B_2 - B_1)^2}$$

Las distancias corresponden a las variaciones que tiene el color A con el color B, lo que suele corresponder a tono, saturación o luminosidad.

A partir de observaciones empíricas sobre las paletas analizadas, propusimos los siguientes rangos aproximados

$$\text{Si } d(\vec{C}_1,\vec{C}_2) \in (0,\,20], \text{ entonces los colores presentan variaciones del mismo tono.}$$

---

$$\text{Si } d(\vec{C}_1,\vec{C}_2) \in (20, \,70], \text{ Son colores de distinto tono, pero que pueden combinar}$$

---

$$\text{Si } d(\vec{C}_1,\vec{C}_2) \in (70, \,150), \text{ Son colores demasiado lejanos}$$

Luego decidimos probar con otro tipo de colores, como azules marinos y vimos que tenian contrastes perfectos con algunos tipos de amarillos. Luego colores casi blancos que tenían como contrastes colores grises, cafés muy oscuros que creaban una armonía. En términos perceptuales, estos ejemplos mostraron que una gran distancia en el espacio LAB no implica necesariamente falta de armonía.

Esta magnitud representa la distancia perceptual del color respecto al gris neutro, y puede interpretarse como una medida conjunta de saturación y desviación luminosa.

$$\vec{P} = (50,0,0)$$

Ahora basado en ese Punto Central del Espacio, podemos tirar las magnitudes

$$Sea \; \vec{V}_n = (L_n - 50, a_n, b_n)$$

Los vectores junto con su diferencia, definen un triángulo en el espacio cromático. Este ángulo cuantifica la relación direccional entre dos colores, independientemente de su intensidad.

$$\theta = \cos^{-1} \left( \frac{\vec{V}_1 \cdot \vec{V}_2} {|\vec{V}_1|\,|\vec{V}_2|} \right)$$

---

Basados en observaciones, propusimos unos rango de ángulos empíricos para la comparación de colores

$$\text{Si } \theta \approx 0° \text{ entonces tienen la misma dirección tonal}$$ $$0° < \theta < 90° \text{ Combinaciones}$$ $$90° < \theta < 180° \text{ Armonía}$$ $$\theta \approx 180° \text{ Contrastes}$$

Conjunto Compatible

Poseíamos el algoritmo para comparar 2 colores, pero ahora necesitabamos que tomando un color C, encontar el conjunto de colores que sea compatible con los valores que pasemos como parámetros para filtrar

Descrito por:

$$S = \left\{ P_i \in \text{Colores} \;\middle|\; d_{\min} < d(P_i, P_n) < d_{\max} \;\land\; \theta_{\min} < \theta(P_i, P_n) < \theta_{\max} \right\}$$

Entonces:

$$\exists\, \{P_1, P_2, \dots, P_k\} \subseteq \text{C} \;\text{/}\; \forall\, P_i \in \{P_1, \dots, P_k\}, \; d_{\min} < d(P_i, P_n) < d_{\max} \;\land\; \theta_{\min} < \theta(P_i, P_n) < \theta_{\max}$$

Ecuación general de distancias

$$d(\vec{P}, \vec{Q}) = \sqrt{\sum_{i=1}^{n} (P_{i} - Q_{i})^2}$$

Ecuación general de Ángulo

$$\vec{O} = (o_1, o_2, \dots, o_n)$$ $$\vec{V}_P = \vec{P} - \vec{O}, \quad \vec{V}_Q = \vec{Q} - \vec{O}$$ $$\theta = \cos^{-1} \left( \frac{ \sum_{i=1}^{n} (P_i - o_i)(Q_i - o_i) }{ \sqrt{\sum_{i=1}^{n} (P_i - o_i)^2} \; \sqrt{\sum_{i=1}^{n} (Q_i - o_i)^2} } \right)$$

Cromovector como sistema ML-ready

Aunque Cromovector nace como una solución determinista basada en geometría y observación empírica, su estructura es naturalmente compatible con técnicas de Machine Learning.

En esencia, Cromovector define:

• Un espacio de características (feature space)
• Una representación vectorial de cada elemento
• Métricas explícitas de similitud y relación
• Parámetros ajustables que pueden aprenderse a partir de datos

Esto lo convierte en un sistema ML-ready desde su diseño, incluso sin utilizar modelos entrenados inicialmente.

---

Representación vectorial como feature embedding

Cada color puede verse como un embedding:

$$\vec{C} = (L, a, b, f_1, f_2, \dots, f_n)$$

Donde las dimensiones adicionales pueden representar:

• Uso interior / exterior
• Nivel de reflexión de luz
• Tiempo de secado
• Tipo de superficie
• Condiciones climáticas
• Preferencias históricas del usuario

Este embedding permite aplicar directamente algoritmos de aprendizaje sin rediseñar la estructura base.

---

Compatibilidad con algoritmos clásicos de ML

Sobre este espacio se pueden aplicar, sin modificaciones estructurales:

• K-Nearest Neighbors (KNN)
  Para recomendación de colores similares, armónicos o contrastantes.

• Clustering (K-Means, DBSCAN)
  Para descubrir familias cromáticas reales basadas en datos y no en cartillas tradicionales.

• Sistemas de recomendación híbridos
  Combinando reglas geométricas (distancia + ángulo) con preferencias aprendidas del usuario.

• Optimización de parámetros
  Ajustando rangos de distancia y ángulo a partir de feedback real de clientes.

En este enfoque, la geometría no compite con el ML, sino que reduce el espacio de búsqueda y mejora la interpretabilidad del modelo.

---

Del sistema determinista al sistema aprendido

Inicialmente, los rangos de distancia y ángulo se definieron empíricamente:

$$(d_{\min}, d_{\max}), \quad (\theta_{\min}, \theta_{\max})$$

A futuro, estos parámetros pueden ser:

• Ajustados mediante aprendizaje supervisado
• Optimizados con reinforcement learning
• Personalizados por usuario o contexto

El sistema pasa entonces de ser un motor de reglas a un modelo adaptativo, sin perder explicabilidad.

---

Usos potenciales más allá de lo arquitectónico

Aunque Cromovector fue diseñado para pintura arquitectónica, el modelo es agnóstico al dominio.

---

Moda y vestimenta

• Extracción de colores dominantes a partir de una foto del usuario
• Generación de paletas personalizadas según tono de piel, cabello y contexto
• Recomendación de prendas armónicas o contrastantes

---

Agricultura y salud vegetal

• Seguimiento del color de hojas como indicador de estrés o enfermedad
• Comparación temporal de vectores cromáticos
• Detección temprana de anomalías en cultivos

---

Interfaces y diseño digital

• Generación automática de paletas accesibles
• Evaluación de contraste perceptual en UI/UX
• Ajuste dinámico de temas visuales

---

Control de calidad industrial

• Comparación cromática entre lotes
• Detección de desviaciones en procesos productivos
• Clasificación automática de defectos visuales

---

Idea clave

Cromovector no intenta reemplazar la teoría clásica del color ni los modelos de Machine Learning.
Su valor está en actuar como puente entre geometría perceptual, datos reales y aprendizaje automático.